Laplace’s rule of succession
1 urn
Consider an urn with $N$ balls from which $R$ are red and $N-R$ are black. We now draw $n$ balls without replacement and find that $r$ balls are red. We denote this data by $D=(n,r)$. Suppose we know $N$ but don’t know $R$. We ask ourselves the following two questions:
- What is the expected fraction of red balls left after observing $D$?
- What is the probability of drawing a red ball on the $(n+1)$th draw after observing $D$?
Our initial background information is denoted by $I$. Part of this is a uniform prior over $R$,
\[p(R|NI) = \frac{1}{N+1} \ \ \ 0 \leq R \leq N\]Question 1
We start with the first question. The expected fraction is given by (see Appendix)
\[\bE\left[\frac{R-r}{N-n} \mid NDI\right] = \frac{r+1}{n+2}.\]Question 2
We denote the event “red at $(n+1)$th draw” by $R_{n+1}$. We have
\[p(R_{n+1}\mid DNI) = \frac{r+1}{n+2}\]Coin flip
Consider a coin that comes up heads a fraction $\theta$. Assuming a uniform prior, and having observed $r$ times heads in $n$ flips, the probability (our belief) that it will come up heads on the $(n+1)$th flip is given by
\[P(H_{n+1}|DI) = \frac{r+1}{n+2}.\]Interpretation
Note that Laplace’s rule of succession can be written in the form
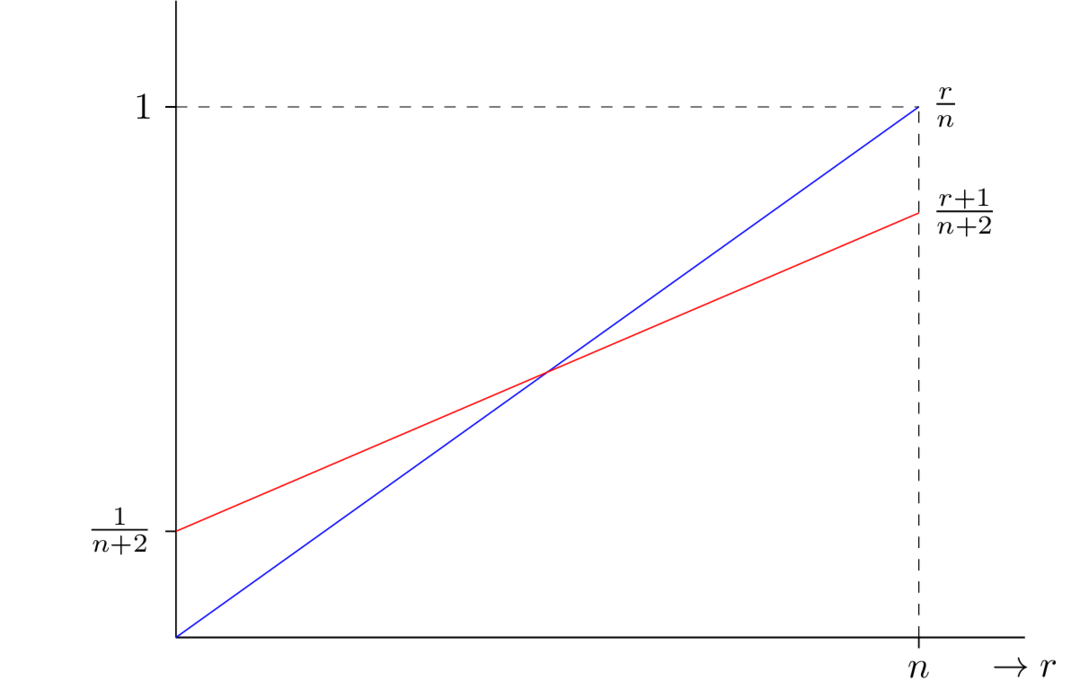
\[\frac{r+1}{n+2} = \frac{n(r/n) + 2(1/2)}{n+2}.\]Note that this can be interpreted as a weighted average of the observation $r/n$ and the prior expectation $1/2$. The data is weighted by $n$ and the prior expectations by $2$. This raises the question, can the prior be interpreted as a posterior distribution resulting from two observations $(n,r) = (2,1)$. The below figure displays how the prior information is pushing the posterior closer to $1/2$.
Appendix
1 urn
Question 1
The posterior of $R$ can be computed using Bayes’ rule.
\[\begin{align} p(R \mid DNI) &= p(R \mid NI) \frac{p(D \mid RNI)}{p(D \mid NI)}\\ &= \binom{N+1}{n+1}^{-1} \binom{R}{r}\binom{N-R}{n-r}, \end{align}\]where we use the following identity:
\[\sum_{R=0}^N \binom{R}{r}\binom{N-R}{n-r} = \binom{N+1}{n+1}.\]Using this identity again, the expectation of $R$ is given by
\[\bE[R \mid DNI] = \frac{(N+2)(r+1)}{(n+2)} - 1.\]And finally the expectation of the fraction is computed as follows:
\[\begin{align*} \bE\left[\frac{R-r}{N-n} \mid NDI\right] &= \frac{\bE[R \mid DNI] - r}{N - n}\\ &= \frac{r+1}{n+2}. \end{align*}\]Question 2
We can compute this by conditioning on $R$.
\[\begin{align*} p(R_{n+1}\mid DNI) &= \sum_{R=0}^N p(R_{n+1}\mid RDNI) p(R \mid DNI)\\ &= \sum_{R=0}^N \frac{R-r}{N-n} \binom{N+1}{n+1}^{-1} \binom{R}{r}\binom{N-R}{n-r}. \end{align*}\]Working this out using the above identity gives
\[p(R_{n+1}\mid DNI) = \frac{r+1}{n+2}.\]coin flip
The probability of the coin coming up heads on the $(n+1)$th throw can be computed as follows
\[\begin{align*} P(H_{n+1}|DI) &= \int_0^1 P(H_{n+1}|\theta DI) p(\theta|DI) d \theta, \\ \end{align*}\]where \(P(H_{n+1}|\theta DI) = \theta.\)
The posterior of $\theta$ is given by
\[\begin{align*} p(\theta|DI) &= p(\theta| I) \frac{P(D|\theta I)}{P(D|I)} \\ p(\theta| I) &= 1 \\ P(D|\theta I) &= \binom{n}{r} \theta^r (1-\theta)^{n-r}. \end{align*}\]We can now use the following identity, called Euler’s integral:
\[\int_0^1 \theta^r (1-\theta)^{n-r} d\theta = \frac{r!(n-r)!}{(n+1)!}\]and get
\[p(\theta|DI) = \frac{(n+1)!}{r!(n-r)!} \theta^r (1-\theta)^{n-r}.\]Going back to our original objective, we get
\[\begin{align*} P(H_{n+1}|DI) &= \int_0^1 P(H_{n+1}|\theta DI) p(\theta|DI) d \theta\\ &= \int_0^1 \theta \frac{(n+1)!}{r!(n-r)!} \theta^r (1-\theta)^{n-r} d\theta. \end{align*}\]Using again Euler’s integral we get
\[\begin{align*} P(H_{n+1}|DI) = \frac{r+1}{n+2}. \end{align*}\]